I stumbled upon lottery statistics which are very useful if you have never come across the gambler's fallacy. On the UK national lottery you pick 6 numbers out of 59 (1-59). Of these 6 numbers are drawn.
I wondered how this plays out in other lottery-like games, and how do I get to verify these numbers. Verify in the sense for example, that the mean of the uniform distribution of lottery draws is what is expected.
First of all we need numbers, lots of numbers.
I was after a readily available dataset and a lottery-like game where there's no current known analysis that I can find with a quick internet search.
First of all we need numbers, lots of numbers. I'm aiming to at least reproduce (most of) the statistics on lottery.co.uk.
I ended up picking Greek Keno named "Kino" because the data is available online for free.
In the Greek version of Keno, you pick up to 12 numbers out of 80 (1-80). Of these 20 numbers are drawn. The pay table is formed in relation to the amount of numbers you've picked against the amount of numbers drawn that match your pick.
For example if you pick 2 numbers, and both of them match then you win €2.5. If one of them matches you win €0.5. However if you pcik 6 numbers, if two of them match, you don't qualify for any winnings.
After downloading and loading the excel spreadsheets, you can find Kino stats below, from 2015 to 2023 for 559_505 draws.
Read about the gambler's fallacy, BeGambleAware and Responsible Gaming.
Frequency Graph
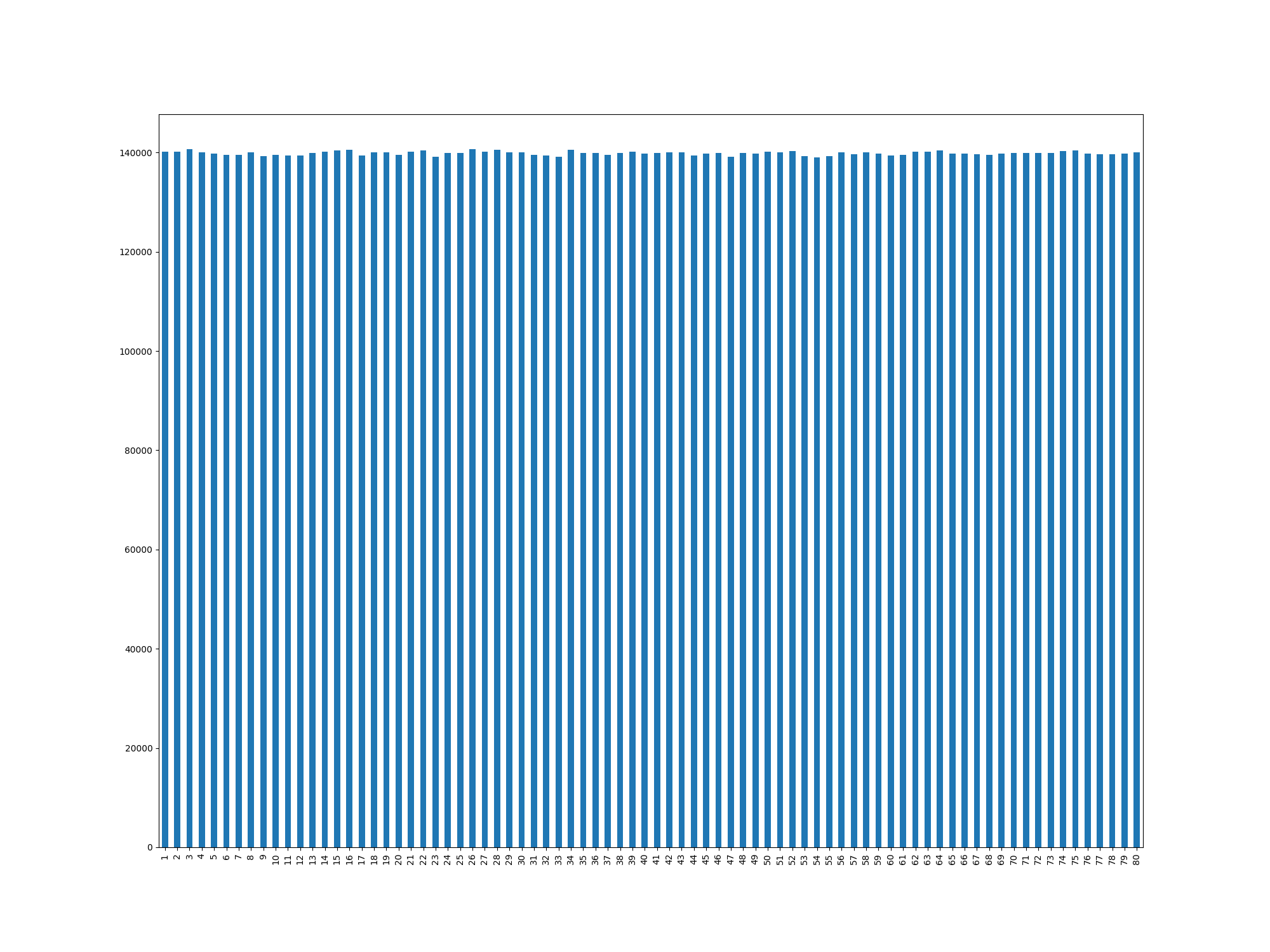
Most common numbers
# Times Drawn
28 140504
34 140519
16 140525
3 140632
26 140687
Least often picked numbers
# Time Drawn
54 139049
47 139115
23 139166
33 139196
55 139257
Most common triplets
3, 26, 34
3, 26, 28
3, 16, 26
3, 15, 26
Most common consecutive pairs
1, 2
79, 80
15, 16
18, 19
26, 27
Most common consecutive triplets
1, 2, 3
78, 79, 80
34, 35, 36
2, 3, 4
14, 15, 16
73, 74, 75
Descriptive Statistics
The numbers at the top indicate the order of the drawn numbers, i.e. for 1, all the numbers that have been drawn first have a mean of 40.46. This is the output from calling describe() on the pandas dataframe.
1 2 3 4 \
count 559505.000000 559505.000000 559505.000000 559505.000000
mean 40.469942 40.514873 40.490982 40.475603
std 23.086179 23.109007 23.112292 23.096609
min 1.000000 1.000000 1.000000 1.000000
25% 21.000000 20.000000 20.000000 20.000000
50% 40.000000 41.000000 40.000000 40.000000
75% 60.000000 61.000000 61.000000 60.000000
max 80.000000 80.000000 80.000000 80.000000
5 6 7 8 \
count 559505.000000 559505.000000 559505.000000 559505.000000
mean 40.477388 40.520717 40.451901 40.476062
std 23.095309 23.104026 23.091244 23.101723
min 1.000000 1.000000 1.000000 1.000000
25% 20.000000 20.000000 20.000000 20.000000
50% 40.000000 41.000000 40.000000 40.000000
75% 61.000000 61.000000 60.000000 61.000000
max 80.000000 80.000000 80.000000 80.000000
9 10 11 12 \
count 559505.000000 559505.000000 559505.000000 559505.000000
mean 40.523447 40.536674 40.514626 40.495322
std 23.092834 23.099860 23.096518 23.116335
min 1.000000 1.000000 1.000000 1.000000
25% 21.000000 21.000000 21.000000 20.000000
50% 40.000000 41.000000 41.000000 40.000000
75% 61.000000 61.000000 61.000000 61.000000
max 80.000000 80.000000 80.000000 80.000000
13 14 15 16 \
count 559505.000000 559505.000000 559505.000000 559505.000000
mean 40.502623 40.503633 40.507095 40.510634
std 23.088596 23.098390 23.094724 23.097256
min 1.000000 1.000000 1.000000 1.000000
25% 21.000000 21.000000 21.000000 21.000000
50% 40.000000 40.000000 40.000000 41.000000
75% 60.000000 61.000000 61.000000 61.000000
max 80.000000 80.000000 80.000000 80.000000
17 18 19 20
count 559505.000000 559505.000000 559505.000000 559505.000000
mean 40.514905 40.445926 40.478031 40.496453
std 23.094424 23.088998 23.070759 23.069527
min 1.000000 1.000000 1.000000 1.000000
25% 21.000000 20.000000 21.000000 21.000000
50% 41.000000 40.000000 40.000000 40.000000
75% 61.000000 60.000000 60.000000 60.000000
max 80.000000 80.000000 80.000000 80.000000
Frequency Table
# Times Drawn
1 140137
2 140219
3 140632
4 140107
5 139789
6 139551
7 139568
8 140095
9 139330
10 139571
11 139371
12 139436
13 139971
14 140205
15 140481
16 140525
17 139383
18 140004
19 140090
20 139587
21 140146
22 140410
23 139166
24 139879
25 139936
26 140687
27 140179
28 140504
29 140041
30 140000
31 139548
32 139418
33 139196
34 140519
35 139883
36 139892
37 139518
38 139864
39 140237
40 139737
41 139868
42 139994
43 140063
44 139436
45 139830
46 139961
47 139115
48 139872
49 139829
50 140115
51 140007
52 140355
53 139289
54 139049
55 139257
56 139994
57 139720
58 140023
59 139763
60 139454
61 139506
62 140186
63 140134
64 140397
65 139743
66 139802
67 139635
68 139592
69 139732
70 139873
71 139952
72 139981
73 139953
74 140312
75 140471
76 139809
77 139709
78 139629
79 139813
80 140065